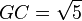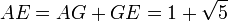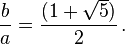El número áureo o de oro (también llamado número plateado, razón extrema y media razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi)Φ (fi) (en mayúscula), en honor al escultor griego Fidias, es un número irracional (en minúscula) o
También se representa con la letra griega Tau (Τ τ), por ser la primera letra de la raíz griega τομή, que significa acortar, aunque encontrarlo representado con la letra Fi (Φ,φ) es más común.
Se trata de un número algebraico irracional (decimal infinito no periódico) que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción entre segmentos de rectas. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza en elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, etc.
Asimismo, se atribuye un carácter estético especial a los objetos que siguen la razón áurea, así como una importancia mística. A lo largo de la historia, se le ha atribuido importancia en diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido objetables para las matemáticas y la arqueología.
Se dice que dos números positivos a y b están en razón áurea si y sólo si:
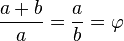
Para obtener el valor de 
a partir de esta razón considere lo siguiente:
a partir de esta razón considere lo siguiente:Que la longitud del segmento más corto b sea 1 y que la de a sea x. Para que estos segmentos cumplan con la razón áurea deben cumplir que:
Multiplicando ambos lados por x y reordenando:
Mediante la fórmula general de las ecuaciones de segundo grado se obtiene que las dos soluciones de la ecuación son
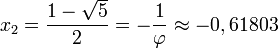
La solución positiva es el valor del número áureo.
El número áureo en la geometría
El número áureo y la sección áurea están presentes en todos los objetos geométricos regulares o semiregulares en los que haya simetría pentagonal, pentágonos o aparezca de alguna manera la raíz cuadrada de cinco.
- Relaciones entre las partes del pentágono.
- Relaciones entre las partes del pentágono estrellado, pentáculo o pentagrama.
- Relaciones entre las partes del decágono.
- Relaciones entre las partes del dodecaedro y del icosaedro.
El rectángulo áureo de Euclides
Euclides obtiene el rectángulo áureo AEFD a partir del cuadrado ABCD. El rectángulo BEFC es asimismo áureo.
El rectángulo AEFD es áureo porque sus lados AE y AD están en la proporción del número áureo. EuclidesLos elementos obtiene su construcción.> en su proposición 2.11 de
Con centro en G se obtiene el punto E, y por lo tanto
resultando evidente que
de donde, finalmente
Por otra parte, los rectángulos AEFD y BEFC son semejantes, de modo que este último es asimismo un rectángulo áureo.
En el pentagrama
El número áureo tiene un papel muy importante en los pentágonos regulares y en los pentagramas. Cada intersección de partes de un segmento, interseca a otro segmento en una razón áurea.
El pentagrama incluye diez triángulos isóceles: cinco acutángulos y cinco obtusángulos. En ambos, la razón de lado mayor y el menor es φ. Estos triángulos se conocen como los triángulos áureos.
Teniendo en cuenta la gran simetría de este símbolo se observa que dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad hasta el infinito. Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande. Al medir la longitud total de una de las cinco líneas del pentáculo interior, resulta igual a la longitud de cualquiera de los brazos de la estrella mayor, o sea Φ. Por lo tanto el número de veces en que aparece el número áureo en el pentagrama es infinito al anidar infinitos pentagramas.
El teorema de Ptolomeo y el pentágono
Claudio Ptolomeo desarrolló un teorema conocido como el teorema de Ptolomeo, el cual permite trazar un pentágono regular mediante regla y compás. Aplicando este teorema un cuadrilátero es formado al quitar uno de los vértices del pentágono, Si las diagonales y la base mayor miden b, y los lados y la base menor miden a, resulta que b2 = a2 + ab lo que implica:
Relación con los sólidos platónicos
El número áureo está relacionado con los sólidos platónicos, en particular con el icosaedro y el dodecaedro, cuyas dimensiones están dadas en términos del número áureo. Los 12 vértices de un icosaedro con aristas de longitud 2, pueden darse en coordenadas cartesianas por los siguientes puntos: (0, ±1, ±φ), (±1, ±φ, 0), (±φ, 0, ±1)
Los 20 vértices de un dodecaedro con aristas de longitud 2/φ=√5−1, también se pueden dar en términos similares: (±1, ±1, ±1), (0, ±1/φ, ±φ), (±1/φ, ±φ, 0), (±φ, 0, ±1/φ)
Para un dodecaedro con aristas de longitud a, su volumen y su área total se pueden expresar también en términos del número áureo:
Si tres rectángulos áureos se solapan paralelamente en sus centros, las 12 esquinas de los rectángulos áureos coinciden exactamente con los vértices de un icosaedro, y con los centros de las caras de un dodecaedro:
El punto que los rectángulos tienen en común es el centro tanto del dodecaedro como del icosaedro.
En este video se puede ver una explicacion mas detallada de el numero de laproporcion divina
